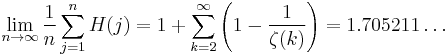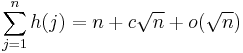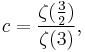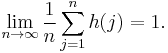Niven's constant

In number theory, Niven's constant, named after Ivan Niven, is the largest exponent appearing in the prime factorization of any natural number n "on average". More precisely, if we define H(1) = 1 and H(n) = the largest exponent appearing in the unique prime factorization of a natural number n > 1, then Niven's constant is given by

$\lim_{n \to \infty} \frac{1}{n} \sum_{j=1}^n H(j) = 1%2B\sum_{k=2}^\infty \left(1-\frac{1}{\zeta(k)}\right) = 1.705211\dots \,$

where ζ(k) is the value of the Riemann zeta function at the point k (Niven, 1969).

In the same paper Niven also proved that

$\sum_{j=1}^n h(j) = n %2B c\sqrt{n} %2B o (\sqrt{n}) \,$

where h(1) = 1, h(n) = the smallest exponent appearing in the unique prime factorization of each natural number n > 1, o is little o notation, and the constant c is given by

$c = \frac{\zeta(\frac{3}{2})}{\zeta(3)}, \,$

and consequently that

$\lim_{n\to\infty} \frac{1}{n}\sum_{j=1}^n h(j) = 1.$

References

Niven, Ivan M. (August 1969). "Averages of Exponents in Factoring Integers". Proceedings of the American Mathematical Society 22 (2): 356–360. doi:10.2307/2037055. JSTOR 2037055.
Steven R. Finch, Mathematical Constants (Encyclopedia of Mathematics and its Applications), Cambridge University Press, 2003

External links

Weisstein, Eric W., "Niven's Constant" from MathWorld.
Sloane's A033150 . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.